1d pml

[psalasiya]

Hi,

I am simulating 1D scalar wave equation in NGSolve with an incident plane wave. I have to use absorbing boundary conditions for which I take help of PML. I have used PML in 2D simulations before and thought 1D implementation would be simpler but I cannot make it work. Here is the line where I implement cartesian PML.

mesh.SetPML(pml.Cartesian(maxs =10, mins = 32.5, alpha=1j), ‘m6’),

where domain of interest is [10, 32.5], material outside this domain is labelled ‘m6’ where PML is to implemented.

Let me know of any mistakes. Appreciate your help.

P.S. Solution

[christopher]

Can you post the example?

[psalasiya]

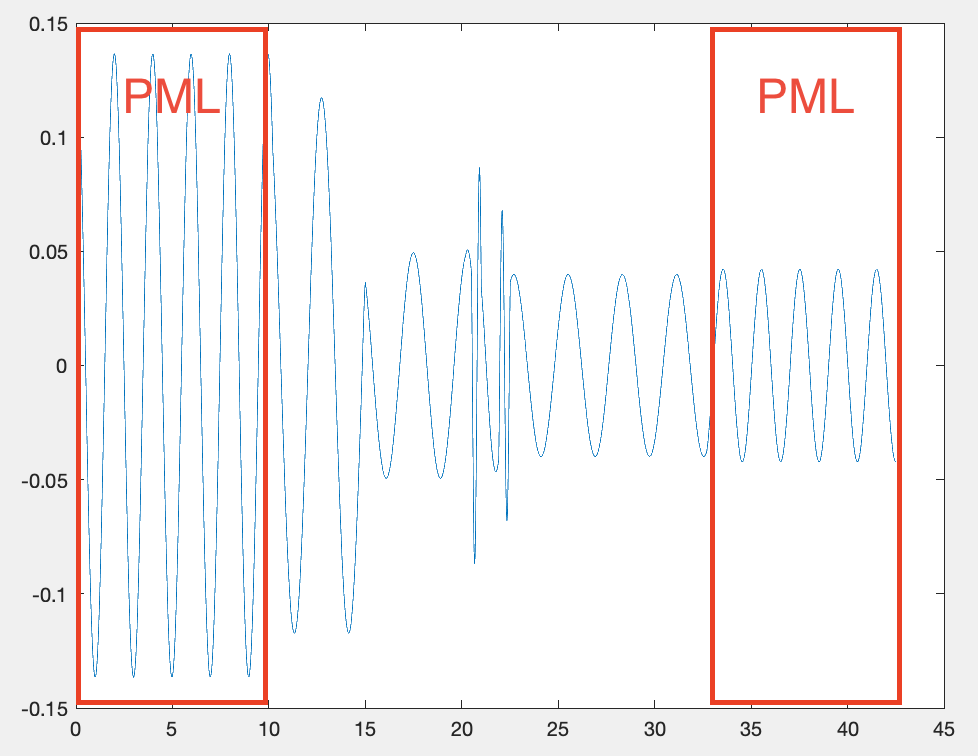
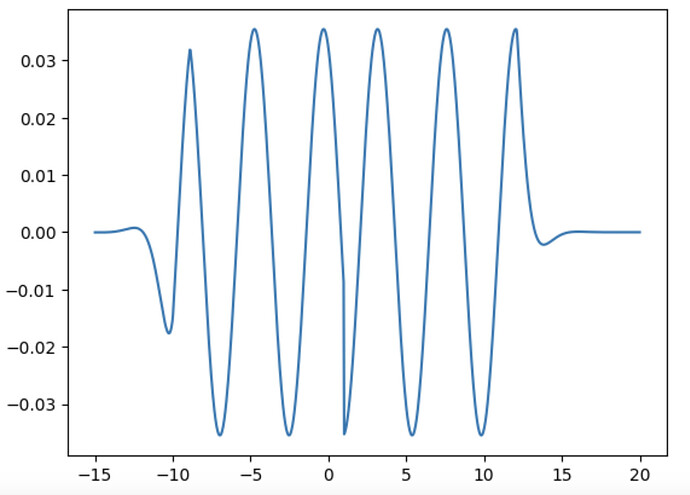
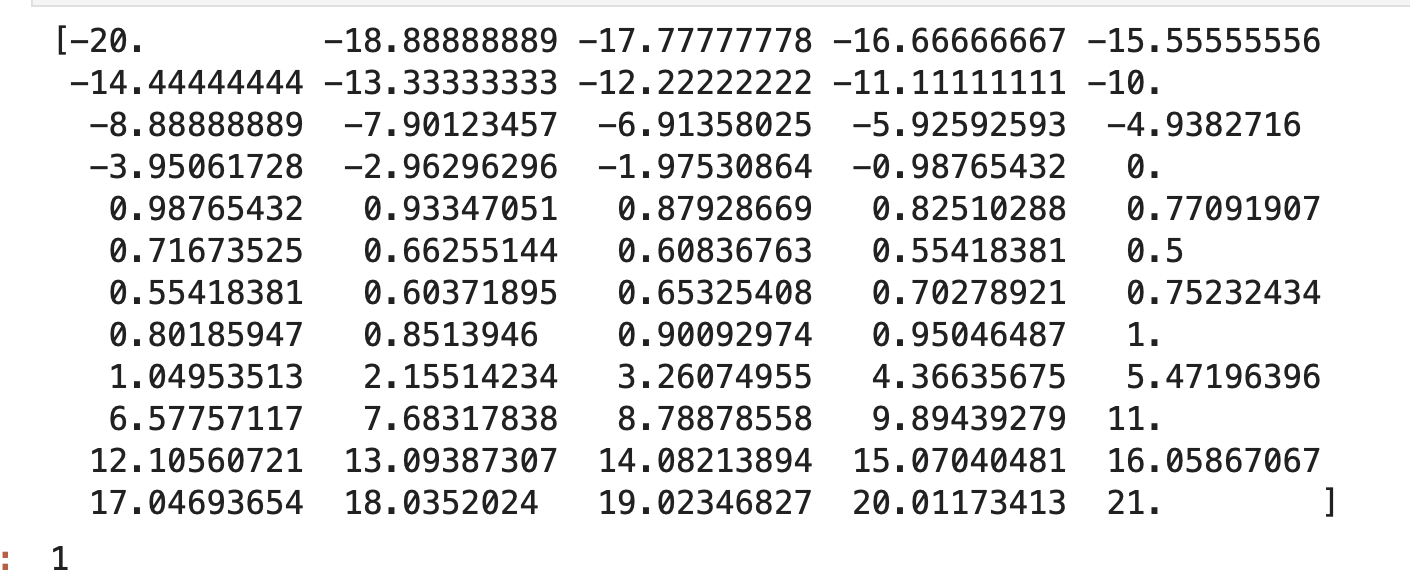
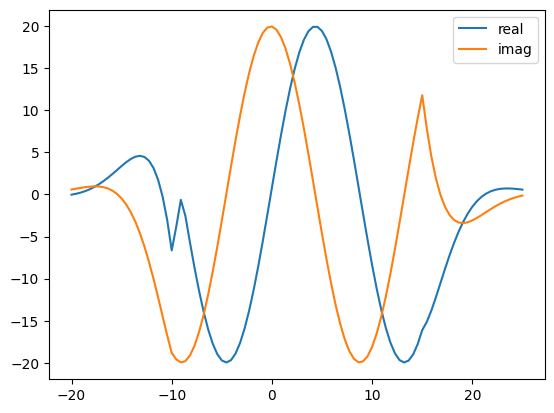
Yes. Here is the 1D wave propagation problem that I am trying to solve. Thank you.

#%%
from ngsolve import *
import ngsolve as ngs
from netgen.meshing import *
import numpy as np
import scipy.io

#%% Geometry
nnodes = 10
part = [-20, -10, 0, 0.5, 1, 11, 21]

n = []
for i in range(len(part) - 1):
    n.append(nnodes)

unit_cell = Mesh(dim = 1)

diff = 0
nodes = np.empty(0)
for i in range(len(n)):
    a = np.linspace(part[i] + diff, part[i + 1], n[i])
    nodes = np.append(nodes, a)
    diff = np.abs(nodes[len(nodes) - 1] - nodes[len(nodes) - 2])
# nodes = np.delete(nodes, 0)

pnums = []
for i in range(sum(n)):
    pnums.append(unit_cell.Add(MeshPoint(Pnt(nodes[i], 0, 0))))

idx1 = unit_cell.AddRegion("pml", dim=1)
idx2 = unit_cell.AddRegion("hom", dim=1)
idx3 = unit_cell.AddRegion("rt1", dim=1)
idx4 = unit_cell.AddRegion("rt2", dim=1)

for i in range(len(nodes)-1):
    if nodes[i] <= part[1]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx1))
    elif nodes[i] > part[1] and nodes[i] <= part[2]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx2))
    elif nodes[i] > part[2] and nodes[i] <= part[3]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx3))
    elif nodes[i] > part[3] and nodes[i] <= part[4]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx4))
    elif nodes[i] > part[4] and nodes[i] <= part[5]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx2))
    elif nodes[i] > part[5] and nodes[i] <= part[6]:
        unit_cell.Add (Element1D([pnums[i], pnums[i+1]], index = idx1))

id5 = unit_cell.AddRegion("l", dim=0)
id6 = unit_cell.AddRegion("r", dim=0)

unit_cell.Add (Element0D(pnums[0] , index=id5))
unit_cell.Add (Element0D(pnums[-1], index=id6))

#%% Meshing
mesh = ngs.Mesh(unit_cell)
mesh.SetPML(pml.Cartesian(mins = -10, alpha=1j, maxs = 11), 'pml')

#%% Materials

rhd = {'pml' : 1, 'hom' : 1, 'rt1' : 1, 'rt2' : 1}
mud = {'pml' : 2, 'hom' : 2, 'rt1' : 2, 'rt2' : 2}

rho = CoefficientFunction([rhd[mat] for mat in mesh.GetMaterials()])
mu  = CoefficientFunction([mud[mat] for mat in mesh.GetMaterials()])

#%% Solution
omega = 2

fes = H1(mesh, order=3, complex=True)
u = fes.TrialFunction()
v = fes.TestFunction()

b = (10**2 / np.pi) * exp(-50**2*((x+7)**2))
    
a = BilinearForm(fes)
a += mu*grad(u)*grad(v)*dx - omega**2*rho*u*v*dx
    
f = LinearForm(fes)
f += b*v*dx # + t*v*ds("dir_neu")
    
a.Assemble()
f.Assemble()
    
gfu = GridFunction(fes)
    
gfu.vec.data += a.mat.Inverse(freedofs=fes.FreeDofs()) * f.vec

1D_wav_prop.py (2.7 KB)

[joachim]

the solution I get from you script does not look that wrong:

I am not sure if you wanted your point distribution like that (going backwards from 1 to 0.5):

here is the notebook I was running from your code:
PML1d.ipynb (48.9 KB)

Joachim

[psalasiya]

Thank you Joachim for your response. Can you explain a bit more on what you mean by point distribution going backwards?

[joachim]

the list n is not sorted

[psalasiya]

Hi Joachim,

I am still not convinced that pml I implemented works. For example, why do I have sharp kink at the right boundary in the imaginary part of the field u where the pml starts? What am I missing. Thank you.

P.S. I have updated the code since my last post so that now the list n is sorted. I am attaching the code for your reference

1dpml.py (2.6 KB)

[joachim]

the 1D elements have point enumeration ‘right point’, ‘left point’, like:

unit_cell.Add (Element1D([pnums[i+1], pnums[i]], index = idx1))

Joachim