Hey,
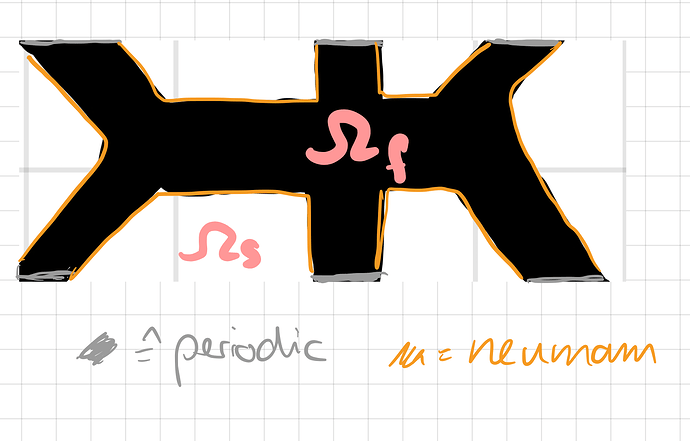
I want have a channel-like geometry (see attached image sketch) where white = solid and black = fluid.
The image is created from a Voronoi Tessellation. So I have access to the vertices that create the network. My question is the following:
I want to solve a Laplace equation on $$\Omega_{fluid}$$, with Neumann boundary conditions between solid and fluid and periodic boundary conditions on the cell boundary (left / right & top / bottom).
My approach is the following:
Using CSG2d()
# Making the geometry
geo = CSG2d()
# Build Square
rect = Solid2d(
[ (0,0), (edge_length,0.0), (edge_length,edge_length), (0.0,edge_length) ], mat='fluid', bc='outer'
)
# generate solid 2d object
cell1 = Solid2d(polygon_vertices1, mat='solid', bc='wall')
cell2 = Solid2d(polygon_vertices2, mat='solid', bc='wall')
# ... put that in a for loop
# final geometry
cells = cell 1 + cell2 # + ...
domain = rect - cells
geo.add(domain)
# set boundary conditions for wall:
normal = specialcf.normal(mesh.dim)
neumann_1 = CoefficientFunction(
[normal[0] if bc == "wall" else 0 for bc in mesh.GetBoundaries()])
# TODO: how to set periodic bc for outer:
Questions:
- Is there a way to set periodic bc with CSG2d()?
- Is there a more elegant way to create the geometry? E.g. use a binary image to determine the domain? Use another type of preprocessing (e.g. find the contours and then create a spline geometry?)