Acceleration in Linear Elasticity

NGSolve
1

Hi everyone,

I’m trying to input acceleration along z axis in a simple linear elasticity problem.
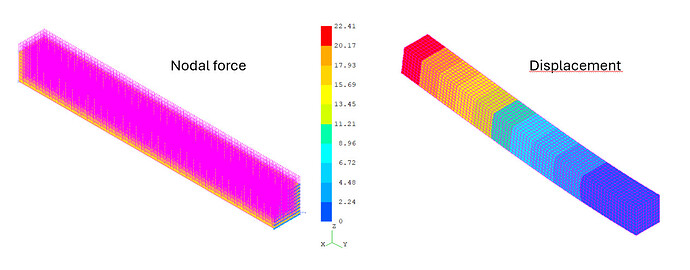
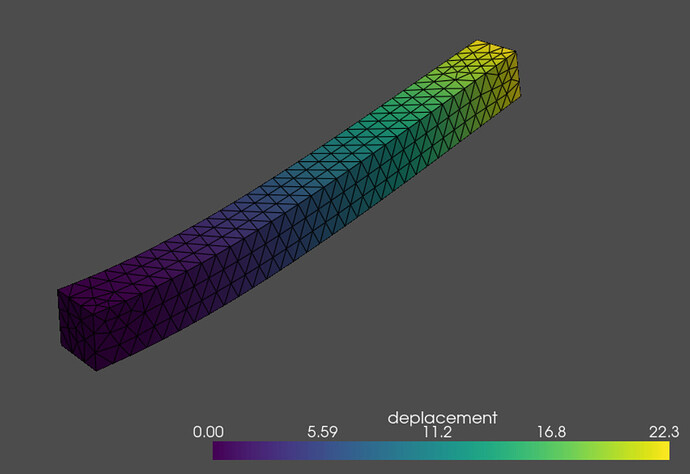
The shape of the result look good, but the displacements are out of range.
I’m shearching for a solution but I’m out of ideas. If you have any solution.

This is my complet code.

from netgen.occ import *
from ngsolve import *
from ngsolve.webgui import Draw

# Variable
E = 210000
nu = 0.3
rho = 7810e-9
acc = 100000 # Acceleration

# Dirichlet Boundaries
Face_Dirichletx = 'Face4'
Face_Dirichlety = 'Face4'
Face_Dirichletz = 'Face4'

# Degree of Element
EleDeg = 2

# Mesh the geometrie and get the boundaries --------------------------------------------------

box = Box((0,-10,-10), (200,10,10))
box.faces.Max(X).name="Face4"
box.faces.Min(X).name="Face2"
geo = OCCGeometry(box)
mesh = Mesh(geo.GenerateMesh(maxh=6)).Curve(3)
boundaries = list(mesh.GetBoundaries())

# Calculation of Acceleration -----------------------------------------------
FonctionVolume = CoefficientFunction(1)
volume = Integrate(FonctionVolume, mesh)
NbNod = mesh.nv
NbMai = mesh.ne
NodeAcc = (rho * volume * acc) / (NbNod)
print("NbNode", NbNod)
print("Volume", volume)
print("mass", rho * volume)
print("NodeAcc", NodeAcc)
ACC = CF((0,0,NodeAcc))

# FE Space ---------------------------------------------------------------------------------
fes = VectorH1(mesh, order=EleDeg, dirichletx=Face_Dirichletx, dirichlety=Face_Dirichlety, dirichletz=Face_Dirichletz)
u, v = fes.TnT()
gfu = GridFunction(fes)

# Stress function ---------------------------------------------------------------------------------
def Stress(strain):
    print("Calculation of Stress")
    mu = E / 2 / (1 + nu)
    lam = E * nu / ((1 + nu) * (1 - 2 * nu))
    return 2 * mu * strain + lam * Trace(strain) * Id(3)

# Assemble of a ----------------------------------------------------------------------------
with TaskManager():
    a = BilinearForm(fes)
    a += SymbolicEnergy(InnerProduct(Stress(Sym(Grad(u))), Sym(Grad(u))))
    pre = Preconditioner(a, "bddc")
    a.AssembleLinearization(gfu.vec)

# Assemble of f with acceleration ---------------------------------------------------------
# f = LinearForm(ACC * v * dx).Assemble()
f = LinearForm(fes)
f += SymbolicLFI(ACC*v)
f.Assemble()

# Run the Solver --------------------------------------------------------------------------
from ngsolve.krylovspace import CGSolver
inv = CGSolver(a.mat, pre, printrates='\r', tol=1e-6, maxiter=500)
gfu.vec.data = inv * f.vec

Draw(gfu)

Thanks in advance.
Thomas

2

Hi Thomas,

to get from acceleration to displacement you have to integrate twice in time. I guess you want to use some time-stepping method for that.

Here is a lecture for solving the scalar wave equation, it is very similar for linear elasticity:
https://jschoeberl.github.io/IntroSC/PDEs/waveequation.html

Joachim

1 Like
3

Hi,

I see what you mean, but I have maybe an easier solution.

I would like to apply a force along the Z axis on every nodes of the mesh.
To calculate the value of this force, I use this expression:

NodalForce = (rho * volume * acc) / (NbNod)

The NodalForce in Newton is called NodAcc in my last code.

I’ve tried this methode in a famous EF code and it work :

image
image1265×495 136 KB

I found the exact same value between the model with acceleration and the model with the nodal loads (linear solver).

In my ngsolve script, I’ve noted that when I change the mesh density, the displacements results change, it mean that the force I’ve introduced is not only on nodes.

How to introduce nodal forces on every nodes ?

Thanks
Thomas.

4

to get acceleration from the force density you want to solve with the mass matrix

5

I don’t understand,
I don’t want to get acceleration from the force density,
I want to know how to apply force on nodes.

6

if i understand you correctly, you can create a gf on a space with order 1 and set the (nodal) values of the vector. them you can use this gf in your higher order problem

7

Hi,

Yes it should work, but how to use the gf in the problem ?
I made a gf like this:

fes = VectorH1(mesh, order=1, dirichletx=Face_Dirichletx, 
dirichlety=Face_Dirichlety, dirichletz=Face_Dirichletz)
NFCF = CF((0,0,NodalForce))
gfu = GridFunction(fes)
gfu.Interpolate(NFCF)

but then I don’t succeed to use it in my f definition:

f = LinearForm(fes)
f += gfu.Interpolate(ACC)
f.Assemble()

How to do it ?

Thanks a lot for your help.
Thomas

8 
f += gfu * v * dx
10

IT WORK !!!

I found my mistake, I thought that dx allowed to integrate on nodes, but in fact, it integrate on volume.

Thanks a lot, Joachim and Christopher for your help and your quick answer.

image
image1065×732 73 KB