Hi,
I am trying to solve a thermally-induced stress-strain relationship in a simple 2D geometry. I have an circle (called “particle”) inside the square (called “electrolyte”). The idea is to apply temperature gradient to the particle, hence expanding it or compressing, and caluculate stress throughout the geometry.
I decided to use a ContactBoundary between particle surface and the electrolyte because in the case of particle compressing, strain in the electrolyte should be zero. When everything is “glued”, compressing particle would “pull down” electrolyte.
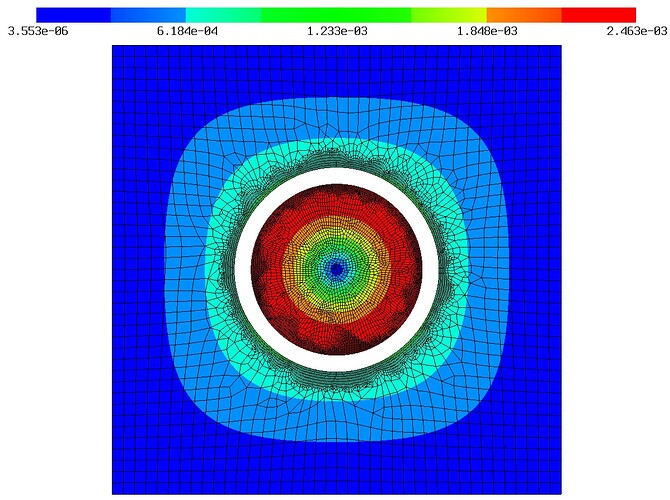
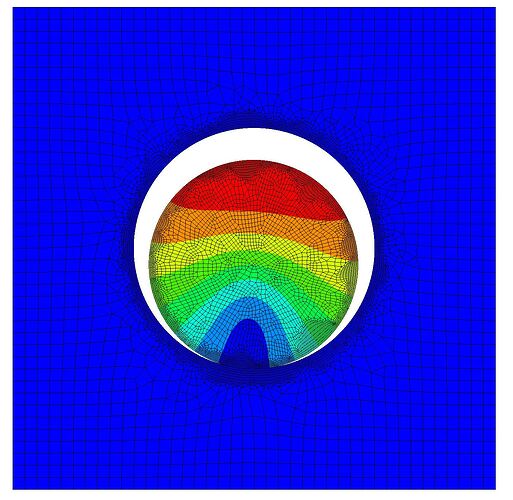
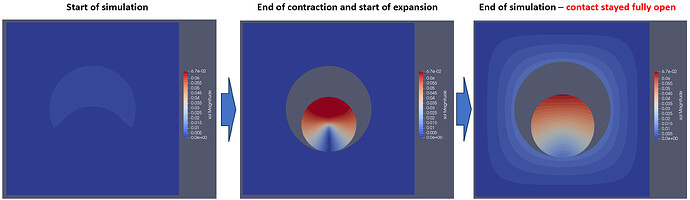
But, when I run the model with some dummy temperature gradients, particle does compress as expected, but the electrolyte is still being pulled down by the particle. This is screenshot with the strain field colored:
When I increase penalty factor for contact optimization, this gap vanishes entirely and I have the same situation as with a glued model, i.e. without contact defined.
Seems that new users cannot upload attachments so I will paste the code for the minimal working example bellow.
For contact definition I was consulting NGSolve examples from 6.2 Contact Problems — NGS-Py 6.2.2601 documentation
I would appreciate if somebody can point me the problem in my contact definition!
Best regards!
CODE:
from ngsolve import *
from netgen.occ import *
from netgen.csg import *
import netgen.gui
def thermal_stress(delta_T, E, nu):
cT = 2e-6
return -E * cT * delta_T / (1 - 2 * nu)
def stress(strain, mu, lam):
return 2 * mu * (strain) + lam * Trace(strain) * Id(2)
def mu(E, nu):
return E / 2 / (1 + nu)
def lam(E, nu):
return E * nu / ((1 + nu) * (1 - 2 * nu))
# Geometry:
rve_width = 4.0
rve_height = 4.0
particle_radius = 1
rect = MoveTo(-rve_width/2, -rve_height/2).Rectangle(rve_width, rve_height).Face()
circle = MoveTo(0, 0).Circle(particle_radius).Face()
particle = MoveTo(0, 0).Circle(particle_radius).Face()
electrolyte = rect - circle
electrolyte.edges.Min(X).name = "left"
electrolyte.edges.Max(X).name = "right"
electrolyte.edges.Min(Y).name = "bottom"
electrolyte.edges.Max(Y).name = "top"
electrolyte.edges[4].name = "contact_ele"
electrolyte.edges[4].maxh = 0.01
particle.edges.name = "contact_par"
electrolyte.faces.name = "electrolyte"
particle.faces.name = "particle"
particle.faces.maxh = 0.04
geo = Compound([electrolyte, particle])
mesh = Mesh(OCCGeometry(geo, dim=2).GenerateMesh(maxh=0.1, quad_dominated=True))
Draw(mesh)
# Mechanical parameters:
E_e, nu_e = 2.10, 0.
E_p, nu_p = 80, 0.
# FE spaces
fes = VectorH1(mesh, order=2, dirichlet="left|right|top|bottom")
fes_particle = VectorH1(mesh, order=2, definedon=mesh.Materials("particle"))
u = fes.TrialFunction()
v = fes.TestFunction()
gfu = GridFunction(fes, "gfu")
dT = GridFunction(fes_particle, "dT") # Temperature gradient
# Contact boundary definition copied from the NGSolve example:
contact = ContactBoundary(
mesh.Boundaries("contact_par"),
mesh.Boundaries("contact_ele")
)
X = CoefficientFunction((x, y))
cf = (X + u - (X.Other() + u.Other())) * (-contact.normal)
contact.AddEnergy(IfPos(cf, cf*cf, 0))
Draw(gfu, mesh, "gfu")
Draw(dT, mesh, "gfc")
a = BilinearForm(fes)
a += SymbolicEnergy(
0.5 * InnerProduct(
stress(Sym(Grad(u)), mu=mu(E_e, nu_e), lam=lam(E_e, nu_e)),
Sym(Grad(u))
), definedon=mesh.Materials("electrolyte")
)
a += SymbolicEnergy(
0.5 * InnerProduct(
stress(Sym(Grad(u)), mu=mu(E_p, nu_p), lam=lam(E_p, nu_p)),
Sym(Grad(u))
), definedon=mesh.Materials("particle")
)
a += SymbolicEnergy(
thermal_stress(dT, E_p, nu_p) *
u, definedon=mesh.Materials("particle")
)
# Two simple dummy steps:
for i in range(2):
dT.Set((-5e3*x, -5e3*y)) # Set dummy temperature gradient
contact.Update(gfu, a)
solvers.NewtonMinimization(a, gfu, printing=False, inverse="sparsecholesky")
print("Step finished!")
print("--------------")
Redraw()