Hello everyone,
I have a problem with DOFs corresponding to higher order basis functions not getting the same index in the gridfunction each time. In my application, computations can take quite some time, so I’d like to save my solutions, so that they can be visualised later.
The way I’m trying to achieve this is as follows: when I compute the solution, the mesh is saved to a .vol-file and the solution gridfunction is saved to a file containing all its coefficients in the right order. Later, when I’d like to load this solution again, I create a new finite element space (which is a product space in my application) using the mesh loaded from the .vol-file, correct dirichlet boundary settings and correct order. Details about how I save the mesh and solution, and how the finite element space is generated are given below.
The trouble is, the DOFs in the new finite element space corresponding to higher (>1) order basis functions seem to be reshuffled. This makes the coefficients corresponding to those DOFs saved in the gridfunction incorrect.
Is there a way to make sure the DOFs in the new finite element space are ordered in the same manner?
Thanks!
Details about how saving and setting up FE space in my code is implemented:
-
Saving the mesh:
mesh.ngmesh.Save(‘folder/mesh.vol’) -
Loading the mesh:
mesh = ngsolve.Mesh(‘folder/mesh.vol’) -
Saving the gridfunction (which has many components):
gf_vec_array = gf.vec.FV().NumPy()
np.save(filename, gf_vec_array) -
Loading the gridfunction:
array = np.load(filename)
gridfunction.vec.FV().NumPy()[:] = array -
Setting up FE space: (self.mesh is the mesh loaded in from the .vol-file, or the one generated at the start of the solution procedure and later saved)
U = ngsolve.H1(self.mesh, order=self.order)
G = ngsolve.H1(self.mesh, order=self.order, dirichlet=BOUNDARY_DICT[SEA])
list_of_spaces = [U for _ in range(2*self.M*(2*self.imax + 1))]
for _ in range(2*self.imax+1):
list_of_spaces.append(G)
X = ngsolve.FESpace(list_of_spaces)
self.femspace = X
Example what goes wrong:
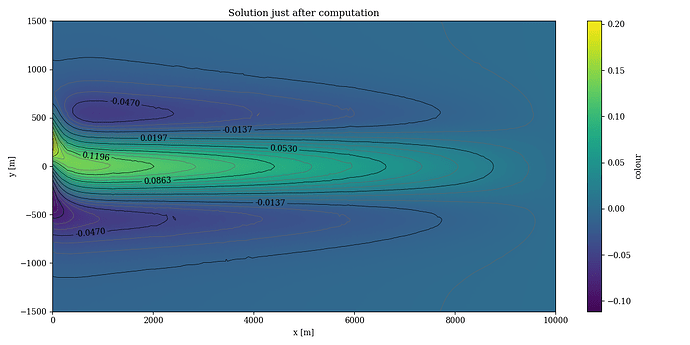
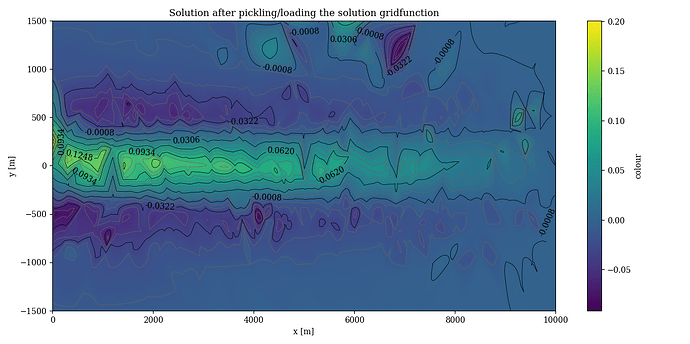
When I tested why my loaded solution looked different than the solution I got when first solving the system, I found the following. For a fourth order basis, the first 312 first order basis functions were ordered in the exact same way. The 313th basis function was different.
By executing the following code and plotting right after solving and after loading the solution in a different file, I found the following figures.
empty_gridfunction = ngsolve.GridFunction(fespace)
empty_gridfunction.components[1].vec[313] = 1
After solving:
After loading: