Hello everyone
That’s the first time I post here, thanks a lot for all the developpement of this code, that’s incredible.
Nowadays, I am intersted in using the HDG versions of the mixed Poisson equation (to compute temperature flux or Darcy flow in porous media).
I have successfully implemented that, so I am happy ![]()
Therefore, my next steps should be to add holes in the mesh but during my investigations, I discover that the results of the flux or the scalar field depends on the type of elements of the mesh (hexa, prism or tet in 3D) and (tri/quad in 2D). The results are perfect for tri/tet elements. Do you have any hint about that?
I did a small modification of the tutorial to build an example with an analytic function.
Elements for a comparison: In this case, the shape of the functions are perfect for all cases except that the magnitude of u is not good.
from ngsolve import *
from ngsolve.webgui import Draw
from meshes import MakeStructured3DMesh
from meshes import MakeStructured2DMesh
test3D = False
testTuto = False
if test3D:
mesh = MakeStructured3DMesh(nx=11,ny=11,nz=11,prism=False,hexes = False)
source = -12 * pi**2 * sin(2 *pi*x)* sin(2 *pi*y)* sin(2 *pi*z)
else:
mesh = MakeStructured2DMesh(nx=51,ny=51,quads = True)
source = -8 * pi**2 * sin(2 *pi*x)* sin(2 *pi*y)
if testTuto:
source = sin(x * pi)
ud = CF(5)
else:
ud = CF(0)
lam = 1
order = 1
V = Discontinuous (HDiv(mesh, order=order))
Q = L2(mesh, order=order-1)
F = FacetFESpace(mesh, order=order, dirichlet="bottom|right|top|left|front|back")
X = V*Q*F
print ("sigmadofs:", X.Range(0))
print ("udofs: ", X.Range(1))
print ("uhatdofs: ", X.Range(2))
sigma,u,uhat = X.TrialFunction()
tau,v,vhat = X.TestFunction()
a = BilinearForm(X, condense=True)
a += (1/lam * sigma*tau + div(sigma)*v + div(tau)*u) * dx
n = specialcf.normal(mesh.dim)
a += (-sigma*n*vhat-tau*n*uhat) * dx(element_boundary=True)
c = Preconditioner(a, "bddc")
f = LinearForm(X)
f += -source*v * dx
a.Assemble()
print ("A non-zero", a.mat.nze)
#print(a.mat)
gfu = GridFunction(X)
gfu.components[2].Set(ud, BND)
f.Assemble()
if a.condense:
fmod = (f.vec + a.harmonic_extension_trans * f.vec).Evaluate()
import numpy as np
inv = a.mat.Inverse(X.FreeDofs(True))
gfu.vec.data += inv * (fmod- a.mat * gfu.vec)
gfu.vec.data += a.harmonic_extension * gfu.vec
gfu.vec.data += a.inner_solve * f.vec
print(np.linalg.norm(fmod))
print(np.linalg.norm(gfu.components[0].vec))
print(np.linalg.norm(gfu.components[1].vec))
print(np.linalg.norm(gfu.components[2].vec))
else:
r = f.vec - a.mat * gfu.vec
inv = a.mat.Inverse(freedofs=X.FreeDofs())
gfu.vec.data += inv * r
Draw (gfu.components[0], mesh, "sigma")
Draw (gfu.components[1], mesh, "u")
vtk = VTKOutput(mesh,coefs=[gfu.components[0],gfu.components[1],source],names=["sigma","u","source"],filename=f"HDG")
vtk.Do()
Here the output to compare solution from quad and triangulation.
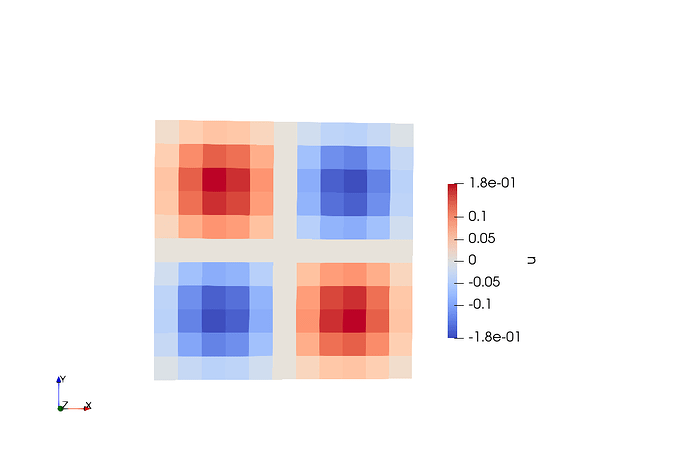
u for Quad
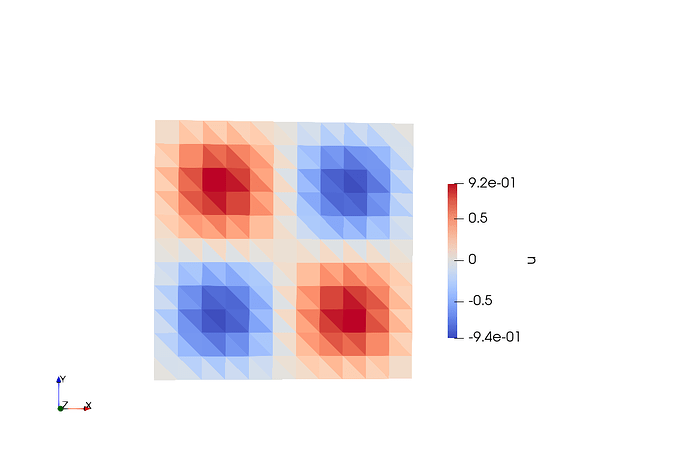
u for Tri
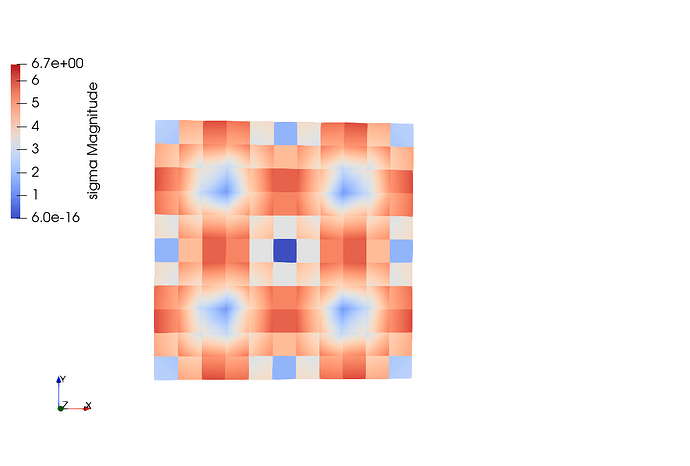
sigma for Quad
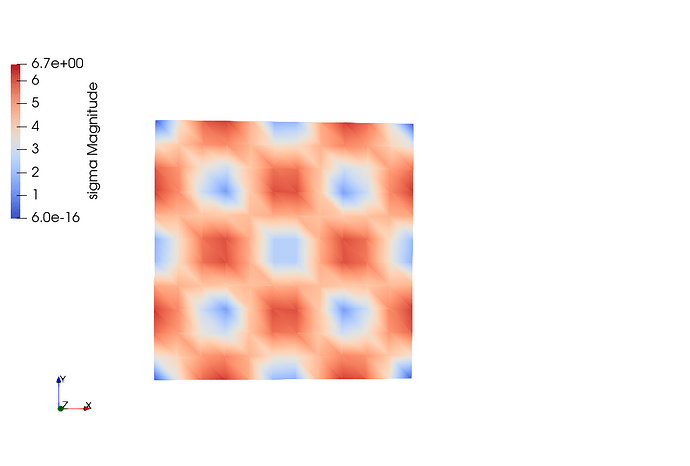
sigma for Tri
Thanks