Hi,
I have two finite element spaces defined as shown below. I solved a problem on one of the boundary edges and now need an operator that maps the solution back into the full space without interpolating the result.
from ngsolve import *
mesh = Mesh(unit_square.GenerateMesh(maxh=1))
fes = HCurl(mesh, order=3)
fes2 = HCurl(mesh, order=3, definedon=mesh.Boundaries('top'))
conv = ConvertOperator(fes, fes2)
print(conv)
For example, suppose the dimension of my full space is m×m and that of the ‘edge space’ is n×n. My solution vector is nx1, and I need to transform it back to mx1. Essentially, I need a vector of size m × 1 with my solution correctly distributed.
The ConvertOperator does not appear to function as I had imagined it would.
Sos
Why not just interpolate here? Since this is an embedding the interpolation is exact.
Hi Christopher,
Thanks for your reply.
I tried that, but perhaps I am doing it wrong. This is how I implemented it.
Bgfu = GridFunction(fes_full, definedon=mesh.Boundaries(boundary_label))
Bgfu.vec.data = bresult
What happens when I draw the grid function is that the fields are no longer localised on the face on which I solved the problem. I don’t know if this is something with the visualisation.
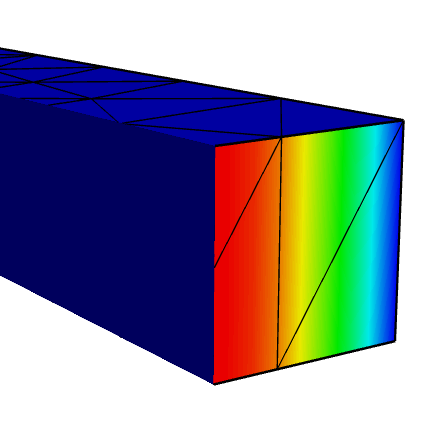
This is the solution visualised on the boundary
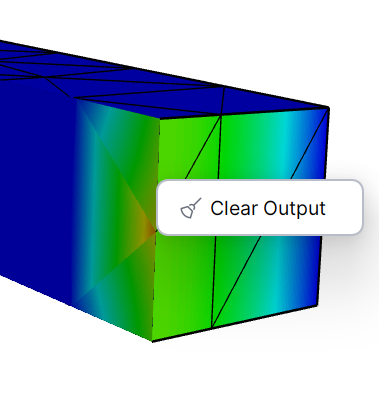
This is the Bgfu (I am guessing interpolated) visualised
The magnitudes are also not the same.
No not setting the vector. The vector sizes are different as the definedon one will skip some not needed basis functions.
Bgfu.Interpolate(bresult, definedon=mesh.Boundaries(boundary_label))
should work
Here is a MWE
from ngsolve import *
from netgen.occ import *
from ngsolve.webgui import Draw
L, a, b = 0.2, 0.1, 0.05
geo = Rectangle(a, b).Face().Extrude(L*Z)
geo.faces.Min(Z).name = “port1”
geo.faces.Max(Z).name = “port2”
mesh = Mesh(OCCGeometry(geo).GenerateMesh(maxh=0.05))
mesh.Curve(3)
fesport = HCurl(mesh, order=3, dirichlet=‘default’, definedon=mesh.Boundaries(‘port2’))
fesfull = HCurl(mesh, order=3, dirichlet=‘default’)
u, v = fesport.TnT()
a = BilinearForm(curl(u.Trace())*curl(v.Trace())*ds(‘port2’))
m = BilinearForm(u.Trace()*v.Trace()*ds(‘port2’))
apre = BilinearForm((curl(u).Trace()*curl(v).Trace() + u.Trace()*v.Trace())*ds(‘port2’))
pre = Preconditioner(apre, type=“direct”, inverse=“sparsecholesky”)
a.Assemble()
m.Assemble()
apre.Assemble()
G, fesh1 = fesport.CreateGradient()
GT = G.CreateTranspose()
math1 = GT @ m.mat @ G
invh1 = math1.Inverse(inverse=“sparsecholesky”, freedofs=fesh1.FreeDofs())
proj = IdentityMatrix(fesport.ndof) - G@invh1@GT@m.mat
projpre = proj@pre
evals, evecs = solvers.PINVIT(a.mat, m.mat, pre=projpre, num=2, maxit=20,
printrates=False)
efield = GridFunction(fesport)
efield.vec.data = evecs[0]
Bgfu = GridFunction(fesfull)
Bgfu.Interpolate(efield, definedon=mesh.Boundaries(‘port2’))
I get the following error: NgException: Element class ngfem::HCurlHighOrderFE<10,class ngfem::HCurlHighOrderFE_Shape,class ngfem::T_HCurlHighOrderFiniteElement<10,class ngfem::HCurlHighOrderFE_Shape<10>,class ngfem::HCurlFiniteElement<2> > > does not support interpolation
Bgfu.Set(bresult, definedon=mesh.Boundaries(boundary_label))
Then Set should work in this case.
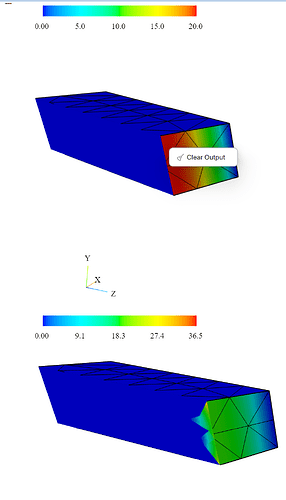
This produces the same result as before when I draw the Norm of efield and Bgfu.
Perhaps this is something with the visualisation. It would be sufficient to know that the exact efield.vec values are copied and arranged appropriately in the bigger vector. However, I compared the non zero values of the arrays from both gridfunction and get different sizes.
ee = efield.vec.FV().NumPy()
ee = ee[np.abs(ee) > 0]
bf = Bgfu.vec.FV().NumPy()
bf = bf[np.abs(bf)>0]
print(bf.shape, ee.shape)
So I am guessing some interpolation is done.
you draw with different scales. if you rescale the surface values should match
Thanks a lot. I also reduced the tolerance for the comparison of the non-zero values to 1e-14 and got the same size.