How to construct a bilinear form of a linear elastic equation?

NGSolve
1

This is my code:

Strain and stress tensor

def strain(u):
return 0.5 * (Grad(u) + Grad(u).trans)
# e(u) = 1/2(Grad(u)+Grad(u)^T)

def stress(u):
return 2mustrain(u) + lamda*Trace(strain(u))*Id(u.dim)

Aε = λ tr(ε)I + 2με , Ae(u) = 2μe(u) + λ div(u)I

Volume constrain

def G(phi):
return Integrate(phi,mesh) - V0

Solve liner elasticity problem with phase field \phi

def solveElasticityProblem(phi):

#define trial- and test- function
u  = fesV.TrialFunction()   #trial function
v = fesV.TestFunction()     #test function

# the right hand side
f = LinearForm(force*v*dx + g*v*ds('BND7')).Assemble() 
    #\int_D f\cdot v dx + \int_Gamma_N g\cdot v ds
    
# the stiffness matrix
a = BilinearForm(fesV, symmetric=False)
a += phi**p*InnerProduct(stress(u), strain(v)) * dx
    ##InnerProduct(div(u)*div(u))  have negtive value, why???
a.Assemble()
    # int_D \rho^p Ae(u):e(v) dx

gfu = GridFunction(fesV)  
gfu.vec.data = a.mat.Inverse(fesV.FreeDofs(),inverse="sparsecholesky")* f.vec

return gfu

ngsolve div problem
ngsolve div problem1939×945 92 KB

2

I don’t understand why the squared of the divergence, interpolated to the grid, would have a negative number

3

Hi Yuanda,
can you post a minimal example? The entries in the vector do not correspond to the field values, but are the coefficients for the basis functions. So negative values do not necessarily mean negative function values.
Best Christopher

4

Dear Christopher,

I hope this email finds you well. First of all, I apologize for not responding sooner. Below is a simple code, and the output result is: “The minimum value of A on the grid is -186.12995756981775.”

Once again, thank you very much for your assistance.

Best regards,
Yuanda Ye

5 
from ngsolve import *
from netgen.geom2d import SplineGeometry
import numpy as np

## Solve the linear elasticity problem of variable density
# \int_D \phi^p * Ae(u):e(v) *dx = \int_D f*v *dx + \int_{\Gamma_N} g*v *ds


## Setting mesh and Finite elements space

#LS=矩形半长边，SS=矩形半短边，FH=短边上分段的点
LS = 1.5
FH = 0.5
SS = 1.0
delta = 0.05
SIZE = 0.05      #mesh size                
                                           #           y
# Set points of boundary    #           |
POINTS = [(LS, SS),          # 2---------|---------1
          (-LS,SS),                  # |            |            |
          (-LS, FH),                 # 3           |           8
          (-LS, -FH),                #-|----------|----------|---->x 
          (-LS, -SS),                # 4           |            7
          (LS, -SS),                 # |            |            |
          (LS, -delta),              # 5---------|----------6
          (LS, delta)]        
GEO = SplineGeometry()      

# Set name of points
P1,P2,P3,P4,P5,P6,P7,P8 = [GEO.AppendPoint(*P) for P in POINTS]
# Set name of boundaries
BNDS = [[["line",P1,P2],"BND1"], 
        [["line",P2,P3],"BND2"],
        [["line",P3,P4],"BND3"],
        [["line",P4,P5],"BND4"],
        [["line",P5,P6],"BND5"],
        [["line",P6,P7],"BND6"],
        [["line",P7,P8],"BND7"], # 牵引力作用于一小段
        [["line",P8,P1],"BND8"],]
# Add boundary to GEO
[GEO.Append(c,bc=bc) for c,bc in BNDS]
# Generate mesh
mesh = Mesh(GEO.GenerateMesh(maxh=SIZE))

# Set boundary condition
DB_MARK= "BND2|BND4"
NB_MARK= ""

## Finite elements space of liner elasticity problem 
fesV = VectorH1(mesh, order = 3, dirichlet = DB_MARK)

## Finite elements space of Allen-Cahn equation 
fesS = H1(mesh, order = 3)

## Initial liner elasticity model parameter
nu      = 0.3
E       = 210
lamda   = nu / ((1+nu)*(1-2*nu))*E  #
mu      = 1 / (2*(1+nu))*E          #
p       = 3 #
phi0    = 0.0001 #


# 设置CF类型的外力函数g
g = CF((0,-10)) #尽管设置在全区域，但只采用边界积分

# volume forve
force = CoefficientFunction( (0,0) )

## define absolution function
Absx = IfPos(x,x,-x)
Absy = IfPos(y,y,-y)

## Initial phi
phi = IfPos(0.08-(Absx-0.75)**2-(Absy-0.5)**2, \
        IfPos(0.08-(Absx-0.75)**2-(Absy-0.5)**2 - phi0,\
            0.08-(Absx-0.75)**2-(Absy-0.5)**2,phi0), 1)
phi_k = GridFunction(fesS)
phi_k.Set(phi)

## Strain and stress tensor
def strain(u):
    return Sym(Grad(u)) 
    # e(u) = 1/2(Grad(u)+Grad(u)^T)

def stress(u):
    return 2*mu*strain(u) + lamda*Trace(strain(u))*Id(u.dim)
    # Aε = λ tr(ε)I + 2με , Ae(u) = 2μe(u) + λ div(u)I

## Solve liner elasticity problem with phase field \phi
print("Being computing displacement field...")
#define trial- and test- function
u  = fesV.TrialFunction()   #trial function
v = fesV.TestFunction()     #test function

# the right hand side
print("   Computing linear form...")
f = LinearForm(force*v*dx + g*v*ds('BND7')).Assemble() 
    #\int_D f\cdot v dx + \int_Gamma_N g\cdot v ds
    
# the stiffness matrix
print("   Computing stiff matrix...")
a = BilinearForm(fesV)
a += phi**p*InnerProduct(stress(u), strain(v)) * dx
    
a.Assemble()
    # int_D \rho^p Ae(u):e(v) dx

gfu = GridFunction(fesV)  # displacement
gfu.vec.data = a.mat.Inverse(fesV.FreeDofs(),inverse="sparsecholesky")* f.vec

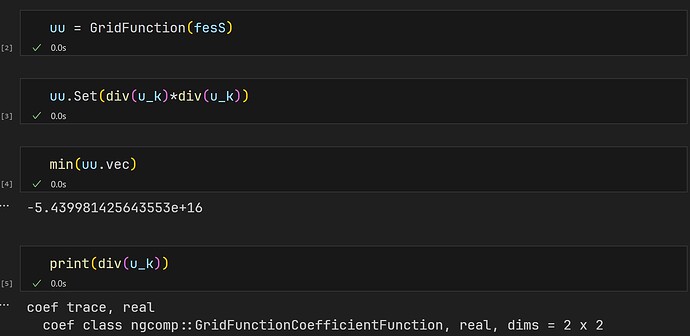
uu = GridFunction(fesS)
uu.Set(div(gfu)*div(gfu))
print(f"The minimum value of A on the grid is {min(uu.vec)}.")
6

Dear Christopher,

First of all, I apologize for not responding sooner. Below is a simple code, and the output result is: “The minimum value of A on the grid is -186.12995756981775.”

Once again, thank you very much for your assistance.

Best regards,
Yuanda Ye

7

You interpolate div(gfu)*div(gfu) into a function space that cannot resolve the order of the argument. so you get an interpolation error.
if you just draw it it is nonnegative.
also second, the values in uu.vec do not represent spacial values of uu, but coefficients with respect to the basis functions. so negative coefficients are not necessarily meaning negative values of uu.

8

Hi Christopher,

I would like to express my sincere gratitude for your prompt and thoughtful response. Your explanation was extremely helpful, and I believe it addresses the issue perfectly. I can confirm that your insights are correct, and I truly appreciate the time and effort you took to assist me.

Thank you once again for your valuable support. I look forward to any further suggestions or guidance you may have.

Best regards,
Yuanda Ye