I am new to NGSolve and still not understand how to constcuct bilinnear form and linear form

[ksugahar]

I am trying to formulate the following equation in NGSolve.

\int {\mu (\nabla v) \cdot (\nabla u)d\Omega } + \int {\mu v({\bf \vec n} \cdot {\bf \vec H}_s )d\Gamma } - \int {\mu (\vec \nabla v) \cdot {\bf \vec H}_s d\Omega }

I started with

u = fes.TrialFunction()
v = fes.TestFunction()
mu_d = {"air" : 1, "magnetic" : 100}
mu = CoefficientFunction([mu_d[mat] for mat in mesh.GetMaterials()])
Hs = CoefficientFunction((0, 1))

a = BilinearForm(fes)
a += mu*grad(u)*grad(v)*dx

f = LinearForm(fes)
f +=  mu*v*InnerProduct(n,Hs)*ds(mesh.Boundaries('out'))
f += -mu*InnerProduct(grad(v),Hs)*dx

a.Assemble()
f.Assemble();

gfu = GridFunction(fes)
gfu.vec.data = a.mat.Inverse(fes.FreeDofs()) * f.vec

But I am not sure how to write second and third term in a correct way.
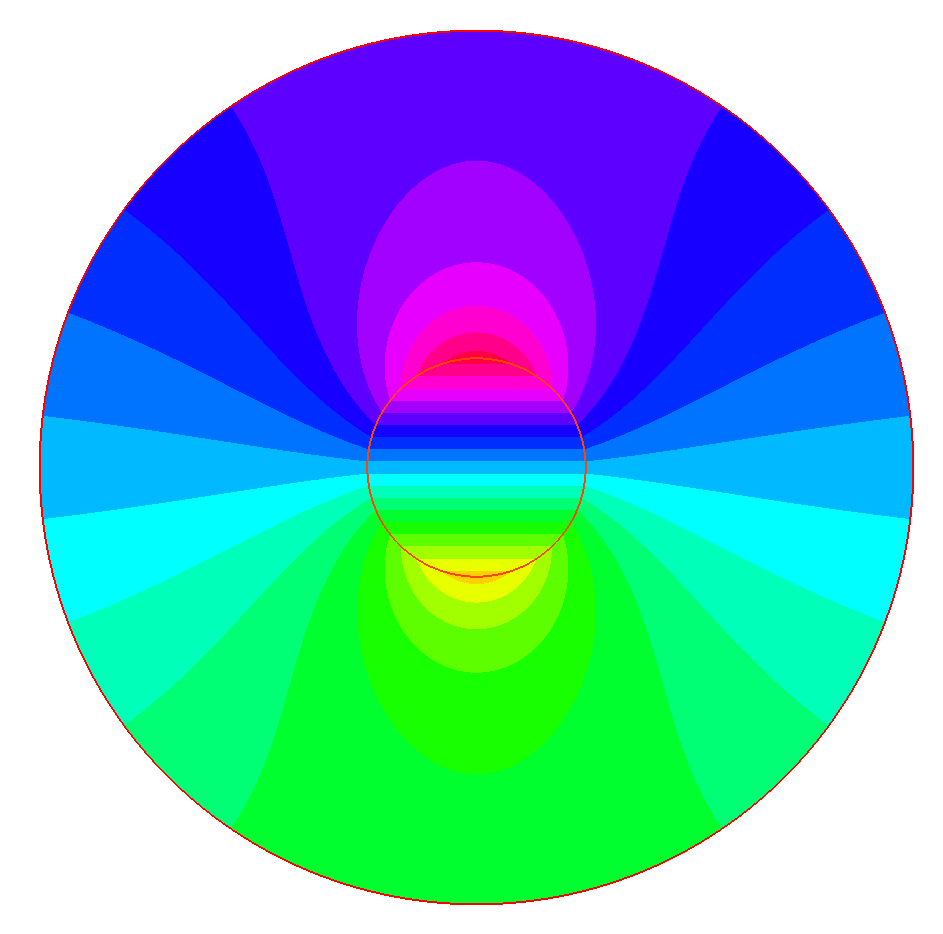
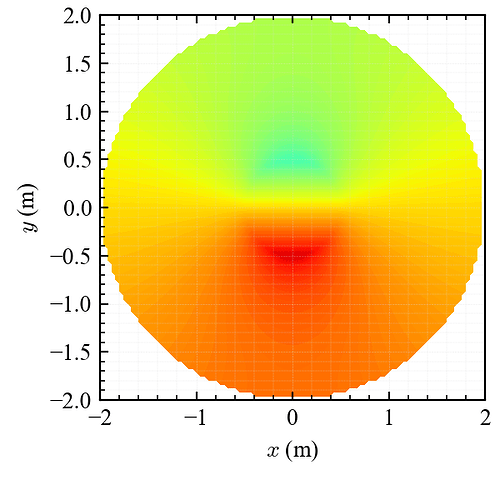
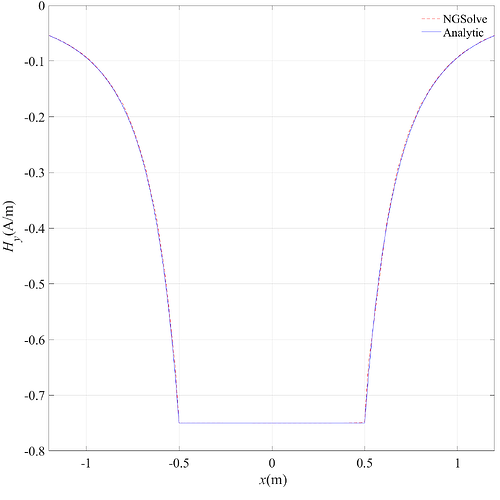
The obtained result seems to be similar with what I solved with FreeFEM++.
Am I doing ok?

[joachim]

Hi Kengo,
there is a problem. The CoefficientFunction HS is defined domain-wise, the index is thought to be the sub-domain index. However, if HS is used in a boundary integral, the index is taken as the boundary number.

A solution is to define

HSb = BoundaryFromVolumeCF(HS)

and use this in the boundary integral. It converts the integration point on the boundary (including boundary number index) to a volume point (and volume number).

help(BoundaryFromVolumeCF) gives good information, in particular what is done on interfaces between different materials.

Best, Joachim

[ksugahar]

Thank you. Joachim,
Even threedimensional case, I could verify my result.
Now I am pretty sure about what I am doing right now.
Kengo.