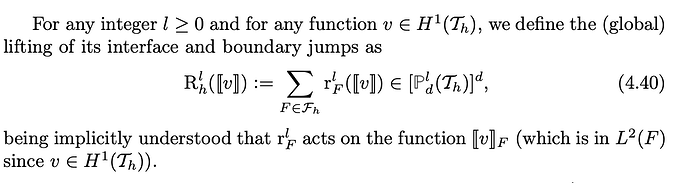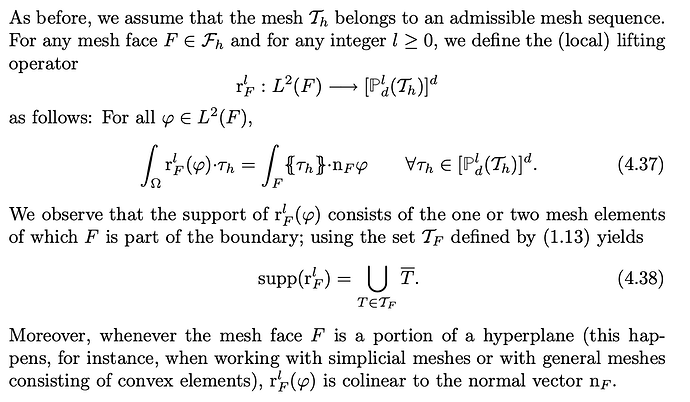Implementing lifting operator in DG

NGSolve
1

Hi,

I am trying to implement a local discontinuous Galerkin (LDG) method for the Laplace equation with homogenous Dirichlet boundary condition. This requires the implementation of a lifting operator. The formulation and the definition of lifting operators are shown in the attached pictures (from the book “Mathematical Aspects of Discontinuous Galerkin Methods” by Di Pietro and Ern).

I have written a working code “LDG_poisson.py” as attached. However, this code is quite slow and clearly not optimal in computational efficiency. I suppose the reason is that I solve a global problem for the lifting R(\jump{phi_i}) of the jumps of basis function phi_i:

\int_{\Omega} R(\jump{phi_i}) \dot \tau = \sum_F \int_{F} (\average{\tau} \dot n_F) \jump{phi_i},

for any test function \tau in the lifting space. In the assembly of stiffness matrix, I have to iterate all the basis function phi_i and solve the lifting R(\jump{phi_i}) , which makes the code quite slow when mesh size is small.

I want to optimize the current code by solving the lifting operator as a local problem, because for any \phi_i supported in an element T the lifting R(\jump{phi_i}) is actually supported in T and its neighboring elements.

I am wondering what would be the best way in NGSolve to solve a local problem as in the attached picture “local_lifting”?

I have tried to compute an integral at a specific edge by a function like this:

def edge_integral(edge,mesh,f): # using 5 points Gauss_lobatto rule
    v=edge.vertices
    v1=np.array(mesh[v[0]].point)
    v2=np.array(mesh[v[1]].point)
    v3=(v1+v2)/2
    v4=v3+(v2-v3)*sqrt(3/7)
    v5=v3-(v2-v3)*sqrt(3/7)
    w1=0.1
    w2=0.1
    w3=32/45
    w4=49/90
    w5=49/90
    len = sqrt((v1[0]-v2[0])**2+(v1[1]-v2[1])**2)
    integral = f(mesh(v1[0],v1[1]))*w1 + f(mesh(v2[0],v2[1]))*w2 + f(mesh(v3[0],v3[1]))*w3 + f(mesh(v4[0],v4[1]))*w4 + f(mesh(v5[0],v5[1]))*w5
    return (len/2)*integral

However, I found calling this function is even slower than the “Integrate” command that computes the integral over the whole domain. I need to compute such an integral for O(1/h^2) times in the assembly of stiffness matrix, and an inefficient computation of local integrals can hinder the speed quite a lot.

I really appreciate in advance any suggestion on the implementation of lifting operator and solving local problems.

Best regards.

discrete_gradient
discrete_gradient1022×284 13.4 KB

global_lifting
global_lifting1240×330 24.2 KB

2024-06-14 11.14.58
2024-06-14 11.14.581292×552 24.7 KB

local_lifting
local_lifting1254×732 52.5 KB

LDG_poisson.py (4.7 KB)

2

you can efficiently evaluate a function on a numpy list of coordinates ,for numpy arrays containing x and y data:

result = f(x,y)

gives you a numpy array and then you can do numpy linalg for efficient evaluation of integrals. Python loops are slow

but you can also just name the edge and then integrate over it:

result = Integrate(f, mesh.Boundaries("bndname"))

in 2d (in 3d it is mesh.BBoundaries(…))

3

Dear Christopher,

Many thanks for your suggestion. I have tried something like

f = CoefficientFunction(1)

x=np.array([0.1,0.2,0.3,0.4,0.5])

y=np.array([0.1,0.2,0.3,0.4,0.5])

print(f(x,y))

and it doesn’t work for me and it has a “incompatible function arguments” warning. I am wondering if this is because the version of NGSolve that I’m using (6.2.2304) is too old. Do I need the latest version of NGSolve for this efficient way of evaluating functions on a list of coordinates?

Many thanks!

Best regards.

4

Sorry, my bad:

f(mesh(x,y))

best