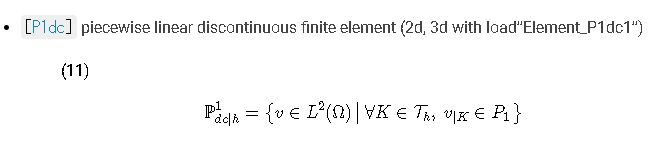When I integrate unit function over circular domain, I obtain the following results.
I am not satisified with the results with H1 element.
Is it possible to define a discontinuous finite element?
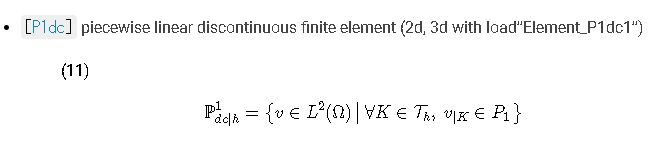
3.1110837354235663::H1 integral
3.1415926547653141::L2 integral
3.1415926535897931::Analytical integral
from netgen.occ import *
from netgen.webgui import Draw as DrawGeo
from numpy import *
from ngsolve import *
from ngsolve.webgui import Draw
wp = WorkPlane()
wp.MoveTo(0, 0).Circle(1)
geo = wp.Face()
geo.name = 'Circle'
geo.maxh = 0.02
wp = WorkPlane()
wp.MoveTo(0, 0).RectangleC(3,3)
geo = Glue([geo, wp.Face()])
#DrawGeo(geo)
mesh = Mesh(OCCGeometry(geo, dim=2).GenerateMesh(meshsize.very_fine)).Curve(3)
Draw(mesh)
fes = H1(mesh, order=4)
J_ = { "Circle" : 1, "default" : 0}
J = GridFunction(fes)
J.Set(CoefficientFunction([ J_[mat] for mat in mesh.GetMaterials() ]))
print(f'{Integrate(J**2*dx(mesh.Materials("Circle")), mesh):20.16f}::H1 integral')
fes = L2(mesh, order=0)
J_ = { "Circle" : 1, "default" : 0}
J = GridFunction(fes)
J.Set(CoefficientFunction([ J_[mat] for mat in mesh.GetMaterials() ]))
print(f'{Integrate(J**2*dx(mesh.Materials("Circle")), mesh):20.16f}::L2 integral')
print(f"{pi:20.16f}::Analytical integral")
With
fes = L2(mesh, order=k)
you define a discontinuous pw polynomial finite element.
Or, you can use the Discontinuous wrapper to make H1 discontinuous
fes = Discontinuous(H1(mesh, order=4))
Best,
Michael
Thank you.
Discontinuous H1 intergral works fine with this case.
\int_0^a {r2\pi rdr} = 2\pi \frac{{a^3 }}{3}
2.0638874605798661::H1 integral
2.0943951040985498::Discontinuous H1 integral
2.0943951040985498::L2 integral
2.0943951023931953::Analytical integral
from netgen.occ import *
from netgen.webgui import Draw as DrawGeo
from numpy import *
from ngsolve import *
from ngsolve.webgui import Draw
wp = WorkPlane()
wp.MoveTo(0, 0).Circle(1)
geo = wp.Face()
geo.name = 'Circle'
geo.maxh = 0.02
wp = WorkPlane()
wp.MoveTo(0, 0).RectangleC(3,3)
geo = Glue([geo, wp.Face()])
#DrawGeo(geo)
mesh = Mesh(OCCGeometry(geo, dim=2).GenerateMesh(meshsize.very_fine)).Curve(3)
Draw(mesh)
fes = H1(mesh, order=4)
J_ = { "Circle" : 1, "default" : 0}
J = GridFunction(fes)
J.Set(CoefficientFunction([ J_[mat]*sqrt(x**2+y**2) for mat in mesh.GetMaterials() ]))
print(f'{Integrate(J*dx(mesh.Materials("Circle")), mesh):20.16f}::H1 integral')
fes = Discontinuous(H1(mesh, order=4))
J_ = { "Circle" : 1, "default" : 0}
J = GridFunction(fes)
J.Set(CoefficientFunction([ J_[mat]*sqrt(x**2+y**2) for mat in mesh.GetMaterials() ]))
print(f'{Integrate(J*dx(mesh.Materials("Circle")), mesh):20.16f}::Discontinuous H1 integral')
fes = L2(mesh, order=4)
J_ = { "Circle" : 1, "default" : 0}
J = GridFunction(fes)
J.Set(CoefficientFunction([ J_[mat]*sqrt(x**2+y**2) for mat in mesh.GetMaterials() ]))
print(f'{Integrate(J*dx(mesh.Materials("Circle")), mesh):20.16f}::L2 integral')
print(f"{2*pi/3:20.16f}::Analytical integral")```