Hi all,
we are trying to solve a problem using a DG method and explicit time stepping. We save the solution of the last time step in a GridFunction u and assemble a BilinearForm with a SymbolicBFI containing u in each time step. u also appears in the DG skeleton integrators. We would like to access the values of u for the degrees of freedom of the neighboring element, just as with ProxyFunction’s .Other(), but this method is not implemented for GridFunctions.
Is there another way to get these values?
Thank you for your help
Alex
Hi Alex,
As you have seen, Other() is only implemented for ProxyFunctions, as the context in which it is used is restricted to SymbolicBFIs of element_boundary or skeleton-type, i.e. whenever the evaluation at an integration point has to take place the neighbor is (automatically) available. This is more cumbersome for general Coefficient/GridFunction as the Evaluation from one integration point (without further context) would need to check if it is on a facet and then ask the mesh for the neighbor, translate the integration point to the neighbors local coordinates, etc…
If you only want to do operator evaluations only, why can’t you formulate the corresponding BilinearForm and use its Apply(·,·) method?
Perhaps you can make an example integral that you want o realize?
Best,
Christoph
Hi Christoph,
I would like to implement the following Integral
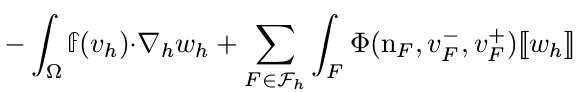
where our flux is f(u)=u*(1-u) (1D for now) and we use for example the Lax-Friedrichs numerical flux
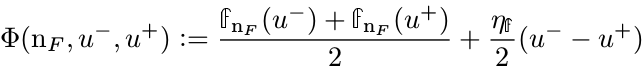 .
.
Here, u[sup]-[/sup] and u[sup]+[/sup] denote the left and right values of u on an interface.
Your are right that we can just use Apply() for a fully explicit time step. But let’s say we want to solve semi-implicitly, I would like to do something like
v = fes.TrialFunction()
w = fes.TestFunction()
u = GridFunction(fes)
a = BilinearForm(fes)
# Lax-Friedrichs, semi-implicit
etaf = abs(n)
phi = 0.5*(v*(1-u) + v.Other(0)*(1-u.Other(0)))*n # error here, u.Other()
phi += 0.5*etaf*(v-v.Other(0))
a += SymbolicBFI(-v*(1-u)*grad(w))
a += SymbolicBFI(phi*(w - w.Other()), skeleton=True)
a += SymbolicBFI(phi*w, BND, skeleton=True)
# .... mass matrix m ...
while t < tend:
a.Assemble()
rhs.data = m.mat * u.vec
mstar.AsVector().data = m.mat.AsVector() + tau * a.mat.AsVector()
invmat = mstar.Inverse(fes.FreeDofs())
u.vec.data = invmat * rhs
Is there an easier solution for this use case?
The obvious (?) solution is to use element_boundary-integrals instead of skeleton-integrals.
Let’s consider only the first part of the integral with
phi = 0.5*(v*(1-u) + v.Other(0)*(1-u.Other(0)))*n
In the skeleton-integrator this gets
phi*(w - w.Other())
However, you can also write this term in terms of element_boundary integrals with
phi = 0.5*v*(1-u)*n
In the element_boundary-integrator this gets
phi*(w - w.Other())
so that the neighboring terms add up to your original term:
0.5*v1*(1-u1)*(w1 - w2)*n1 + 0.5*v2*(1-u2)*(w2 - w1)*n2
= 0.5*(v1*(1-u1)+v2*(1-u2))*(w1 - w2)*n1
Does this help?
Best,
Christoph
Thank you for the idea: element_boundary would indeed work for the example I posted. Unfortunately, I lied about the boundary term (sorry :S ). We actually need
phi = 0.5*(v*(1-u) + v.Other(0)*(1-u.Other(0)))*n
phi += 0.5*(v-v.Other(0))
phiR = IfPos(n, n*IfPos(u-0.5, 0.25, u*(1-u)), 0)
a += SymbolicBFI(-v*(1-u)*grad(w))
a += SymbolicBFI(phi*(w - w.Other()), skeleton=True)
a += SymbolicBFI(phiR*w, BND, skeleton=True)
Am I wrong, or is there no way to restrict element_boundary integrals to inner facets? I guess I could subtract the wrong boundary contribution from element_boundary in a skeleton integrator…
phi = 0.5*(v*(1-u))*n
phi += 0.25*(v-v.Other(0))
phiR = IfPos(n, n*IfPos(u-0.5, 0.25, u*(1-u)), 0)
a += SymbolicBFI(-v*(1-u)*grad(w))
a += SymbolicBFI(phi*(w - w.Other()), element_boundary=True)
a += SymbolicBFI(-1*phi*w, BND, skeleton=True)
a += SymbolicBFI(phiR*w, BND, skeleton=True)
…but that seems very hacky.
As of now, there is no VOL_or_BND-like term for the element_boundary integrals. Another work around would be to use FacetFESpace-GridFunction (order=0) as an indicator for interior or boundary facet, but that is not much less hacky.
Hi, I think we cannot do it directly quite now, but I see two solutions with reasonable effort:
-
Add the Other() operator also to CoefficientFunctions. It becomes a new node in the evaluation tree . We store the ‘other’ MappedIntegrationRule within the ‘this’ MappedIntegrationrule. On evaluating the OtherCoefficientFunction the intrules are swapped. If proxies appear within the other - subtree we need special treatment - I would exclude it for the first implementation.
-
The Apply and the AssembleLinearization is working quite now, right ? The problem comes only from the semi-linearization, where we differentiate some terms with respect to the trial-function, but we freeze the trial-function at some other places (and want to use the GridFunction instead). We could add a Freeze - function, which throws away the derivatives of the sub-tree.
Then Alex code would look like
v = fes.TrialFunction()
u = Freeze(v)
What do you think ? How do we continue ?
Solution 1 (which will find more users soon) needs changes in the core code, I may find some time during the coming week for that, and you can test.
Solution 2 is additive and can be done by Alex, but I think it is quite special purpose.
Joachim
I have added the Other() operator for ordinary CFs.
Pls try it, it’s tested only for a few simple cases by now, and certainly it needs some fixes.
Compile is not supported (Compile(True) throws, and Compile(False) falls back to standard evaluation).
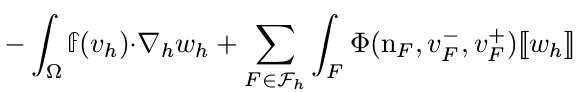
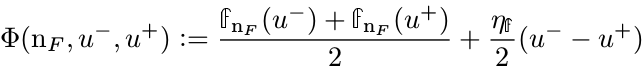 .
.