Hello, I’m looking for the way to intersect overlapped particles.
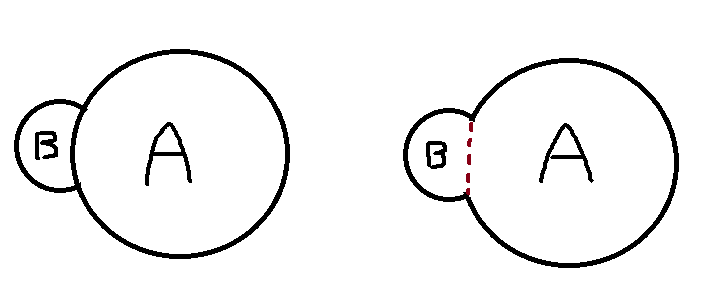
Here is an illustration for description.
Currently, I generate the particle A and B (considering overlapped part, 100% A and 80-90% B, I think).
What I really want to do is “Right image” (overlapped parts are assigned to both A and B).
If I generate the particles with “Union” feature, I cannot differentiate which one is A or B.
I want to Particle A and Particle B as separated domains, and intersected interface between them.
Can you tell me which part in my code should be modified for what I want?
For your information, I wrote down my code and attached some text files.
##################################
# Two particles
##################################
"""
The constructive solid geometry (CSG) format allows to define geometric primitives such as
spheres and cylinders and perform to boolean operations on them.
"""
import numpy as np
import time
from netgen.csg import *
from netgen.meshing import *
import netgen.gui
from ngsolve import ngsglobals
ngsglobals.msg_level = 2
# Generate brick and mesh it
geo1 = CSGeometry()
cube = OrthoBrick( Pnt(0,0,0), Pnt(64,64,64) )
geo1.Add(cube)
m1 = geo1.GenerateMesh (meshsize.moderate, maxh=5)
# m1.Refine()
# Read Coordinates_XYZ_P1, AxisLength_abc_P1, and Euler Angles from *.txt files.
Coordinates_XYZ_P1 = np.loadtxt("outputs/PackingAlgorithm/Centroid_P1.txt")
Coordinates_XYZ_MO_P1 = np.loadtxt("outputs/PackingAlgorithm/Coordinates_XYZ_MO_P1.txt")
AxisLength_abc_P1 = np.loadtxt("outputs/PackingAlgorithm/AxisLength_P1.txt")
Periodicity_O_P1 = np.loadtxt("outputs/PackingAlgorithm/Periodicity_O_P1.txt")
Periodicity_MO_P1 = np.loadtxt("outputs/PackingAlgorithm/Periodicity_MO_P1.txt")
Coordinates_XYZ_P2 = np.loadtxt("outputs/PackingAlgorithm/Centroid_P2.txt")
Coordinates_XYZ_MO_P2 = np.loadtxt("outputs/PackingAlgorithm/Coordinates_XYZ_MO_P2.txt")
AxisLength_abc_P2 = np.loadtxt("outputs/PackingAlgorithm/AxisLength_P2.txt")
Periodicity_O_P2 = np.loadtxt("outputs/PackingAlgorithm/Periodicity_O_P2.txt")
Periodicity_MO_P2 = np.loadtxt("outputs/PackingAlgorithm/Periodicity_MO_P2.txt")
# Make Ellipsoids based on given information
t0_start = time.time()
geo2 = CSGeometry()
##################################
# Ellipsoids from original coordinates
##################################
ellips_O_P1 = [0] * len(Coordinates_XYZ_P1[:,0])
for i in range(0,len(ellips_O_P1)):
# Pnt -> Center point, Vec -> Half of Axis Length
ellips_O_P1[i] = Ellipsoid(Pnt(Coordinates_XYZ_P1[i,0],Coordinates_XYZ_P1[i,1],Coordinates_XYZ_P1[i,2]),
Vec(AxisLength_abc_P1[i,0],0,0),
Vec(0,AxisLength_abc_P1[i,1],0),
Vec(0,0,AxisLength_abc_P1[i,2]))
ellips_O_P2 = [0] * len(Coordinates_XYZ_P2[:,0])
for i in range(0,len(ellips_O_P2)):
# Pnt -> Center point, Vec -> Half of Axis Length
ellips_O_P2[i] = Ellipsoid(Pnt(Coordinates_XYZ_P2[i,0],Coordinates_XYZ_P2[i,1],Coordinates_XYZ_P2[i,2]),
Vec(AxisLength_abc_P2[i,0],0,0),
Vec(0,AxisLength_abc_P2[i,1],0),
Vec(0,0,AxisLength_abc_P2[i,2]))
##################################
# Ellipsoids from matched coordinates
##################################
ellips_MO_P1 = [0] * len(Coordinates_XYZ_MO_P1)
for i in range(0,len(ellips_MO_P1)):
# Pnt -> Center point, Vec -> Half of Axis Length
ellips_MO_P1[i] = Ellipsoid(Pnt(Coordinates_XYZ_MO_P1[i,0], Coordinates_XYZ_MO_P1[i,1], Coordinates_XYZ_MO_P1[i,2]),
Vec(AxisLength_abc_P1[int(Coordinates_XYZ_MO_P1[i,3]),0],0,0),
Vec(0,AxisLength_abc_P1[int(Coordinates_XYZ_MO_P1[i,3]),1],0),
Vec(0,0,AxisLength_abc_P1[int(Coordinates_XYZ_MO_P1[i,3]),2]))
ellips_MO_P2 = [0] * len(Coordinates_XYZ_MO_P2)
for i in range(0,len(ellips_MO_P2)):
# Pnt -> Center point, Vec -> Half of Axis Length
ellips_MO_P2[i] = Ellipsoid(Pnt(Coordinates_XYZ_MO_P2[i,0], Coordinates_XYZ_MO_P2[i,1], Coordinates_XYZ_MO_P2[i,2]),
Vec(AxisLength_abc_P2[int(Coordinates_XYZ_MO_P2[i,3]),0],0,0),
Vec(0,AxisLength_abc_P2[int(Coordinates_XYZ_MO_P2[i,3]),1],0),
Vec(0,0,AxisLength_abc_P2[int(Coordinates_XYZ_MO_P2[i,3]),2]))
##################################
# Ellipsoids for Periodicity_O
##################################
ellips_Periodicty_O_P1 = [0] * len(Periodicity_O_P1)
for i in range(0,len(ellips_Periodicty_O_P1)):
ellips_Periodicty_O_P1[i] = Ellipsoid(Pnt(Periodicity_O_P1[i,0],Periodicity_O_P1[i,1],Periodicity_O_P1[i,2]),
Vec(AxisLength_abc_P1[int(Periodicity_O_P1[i,3]),0],0,0),
Vec(0,AxisLength_abc_P1[int(Periodicity_O_P1[i,3]),1],0),
Vec(0,0,AxisLength_abc_P1[int(Periodicity_O_P1[i,3]),2]))
ellips_Periodicty_O_P2 = [0] * len(Periodicity_O_P2)
for i in range(0,len(ellips_Periodicty_O_P2)):
ellips_Periodicty_O_P2[i] = Ellipsoid(Pnt(Periodicity_O_P2[i,0],Periodicity_O_P2[i,1],Periodicity_O_P2[i,2]),
Vec(AxisLength_abc_P2[int(Periodicity_O_P2[i,3]),0],0,0),
Vec(0,AxisLength_abc_P2[int(Periodicity_O_P2[i,3]),1],0),
Vec(0,0,AxisLength_abc_P2[int(Periodicity_O_P2[i,3]),2]))
##################################
# Ellipsoids for Periodicity_MO
# Exclude overlapped elements based on Periodicity_O_P1 and Periodicity_O_P2
##################################
ellips_Periodicty_MO_P1 = [0] * len(Periodicity_MO_P1)
for i in range(0,len(ellips_Periodicty_MO_P1)):
ellips_Periodicty_MO_P1[i] = Ellipsoid(Pnt(Periodicity_MO_P1[i,0],Periodicity_MO_P1[i,1],Periodicity_MO_P1[i,2]),
Vec(AxisLength_abc_P1[int(Periodicity_MO_P1[i,3]),0],0,0),
Vec(0,AxisLength_abc_P1[int(Periodicity_MO_P1[i,3]),1],0),
Vec(0,0,AxisLength_abc_P1[int(Periodicity_MO_P1[i,3]),2]))
ellips_Periodicty_MO_P2 = [0] * len(Periodicity_MO_P2)
for i in range(0,len(ellips_Periodicty_MO_P2)):
ellips_Periodicty_MO_P2[i] = Ellipsoid(Pnt(Periodicity_MO_P2[i,0],Periodicity_MO_P2[i,1],Periodicity_MO_P2[i,2]),
Vec(AxisLength_abc_P2[int(Periodicity_MO_P2[i,3]),0],0,0),
Vec(0,AxisLength_abc_P2[int(Periodicity_MO_P2[i,3]),1],0),
Vec(0,0,AxisLength_abc_P2[int(Periodicity_MO_P2[i,3]),2]))
##################################
# Store all ellipsoids.
##################################
all_ellips_P1 = ellips_O_P1[0]
all_ellips_P2 = ellips_O_P2[0]
# Modifying the number of elliposids which you want.
for i in range(1,len(ellips_O_P1)):
all_ellips_P1 = all_ellips_P1 + ellips_O_P1[i]
for i in range(0,len(ellips_MO_P1)):
all_ellips_P1 = all_ellips_P1 + ellips_MO_P1[i]
for i in range(0,len(ellips_Periodicty_O_P1)):
all_ellips_P1 = all_ellips_P1 + ellips_Periodicty_O_P1[i]
for i in range(0,len(ellips_Periodicty_MO_P1)):
all_ellips_P1 = all_ellips_P1 + ellips_Periodicty_MO_P1[i]
for i in range(1,len(ellips_O_P2)):
all_ellips_P2 = all_ellips_P2 + ellips_O_P2[i]
for i in range(0,len(ellips_MO_P2)):
all_ellips_P2 = all_ellips_P2 + ellips_MO_P2[i]
for i in range(0,len(ellips_Periodicty_O_P2)):
all_ellips_P2 = all_ellips_P2 + ellips_Periodicty_O_P2[i]
for i in range(0,len(ellips_Periodicty_MO_P2)):
all_ellips_P2 = all_ellips_P2 + ellips_Periodicty_MO_P2[i]
# Intersection between all ellipsoids and cube.
Partial_P1 = all_ellips_P1 * cube
Partial_P2 = all_ellips_P2 * cube
Partial_P2 = Partial_P2 - Partial_P1
# Add components for meshing.
geo2.Add(cube-(Partial_P1+Partial_P2))
geo2.Add(Partial_P1)
geo2.Add(Partial_P2)
m2 = geo2.GenerateMesh (meshsize.moderate)
t0_end = time.time()
print("Making ellipsoids took --- %s seconds ---" % (t0_end - t0_start))
t1_start = time.time()
# Need a NGSolve mesh for visualization.
import ngsolve
mesh = ngsolve.Mesh(m2)
t1_end = time.time()
print("GenerateMesh took --- %s seconds ---" % (t1_end - t1_start))
PackingAlgorithm.zip (8.8 KB)