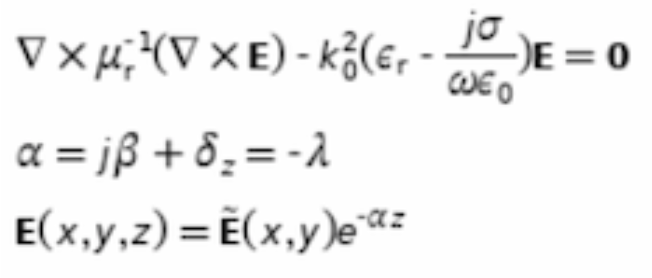Hi,
I am trying to compute the modes propagating in a ridge waveguide. In other words I am trying to reproduce this: https://www.comsol.com/blogs/mode-analysis-for-electromagnetic-waveguides-in-comsol/ .
I have also attached a screenshot with the equations I want to solve. There, \alpha is the eigenvalue I want to solve for (together with the eigenvectors, which give me the spatial profile of the modes). Since, I am only interested in the transverse profile of the modes, I am working with a 2D-mesh, where it is bounded on all sides by a PML, since the modes can leak out of the waveguide.
My question is now: How do I implement the “constraint” that \mathbf{E}(x,y,z) = mathbf{\tilde{E}}(x,y)e^{-\alpha z} and E_z=0?
Thank you very much!