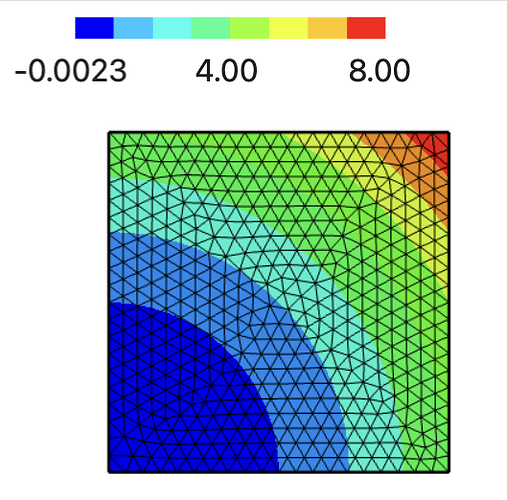
Hi, I was trying to implement Nitsche boundary penatly method on a deformed mesh and stumbled across what could be a bug.
An example for the Poisson equation is the following
from ngsolve import *
from netgen.geom2d import unit_square
from ngsolve.webgui import Draw
mesh = Mesh(unit_square.GenerateMesh(maxh=0.05))
order = 1
V = H1(mesh, order=order)
u, v = V.TnT()
dX = GridFunction(VectorH1(mesh))
dX.Set(CF((x, y)))
n = specialcf.normal(2)
h = specialcf.mesh_size
penalty = 10
u_ex = x**2+y**2
f = -u_ex.Diff(x).Diff(x) - u_ex.Diff(y).Diff(y)
a = BilinearForm(V, symmetric=True)
a += grad(u)*grad(v)*dx(deformation=dX)
a += (-n*grad(u)*v )*ds(deformation=dX, skeleton=True)
a += (-n*grad(v)*u)*ds(deformation=dX, skeleton=True)
a += (penalty/h*u*v)*ds(deformation=dX, skeleton=True)
a.Assemble()
l = LinearForm(V)
l += f* v * dx(deformation=dX)
l += ( -n*grad(v)*u_ex)*ds(deformation=dX, skeleton=True)
l += ( penalty/h*u_ex*v)*ds(deformation=dX, skeleton=True)
l.Assemble()
u = GridFunction(V)
u.vec.data = a.mat.Inverse(freedofs = V.FreeDofs()) * l.vec
Draw(u)
It seems like some penalty terms ignore the deformation flag. Using mesh.SetDeformation(dX) before the assembly instead leads to the correct result.
Thanks,
Alessandro