Hello,
I am relatively new to NGSolve, and came of from studying FEniCS.
I am trying to time-step a weak form that involves two coupled PDEs, to solve for two variables, using the implicit Euler method.
To my understanding, in all tutorials and demos on the NGSolve website (section 3.1-3.5), the authors define the mass matrix as the product of the trial and test function. However, how do I define the mass matrix when two variables are solved for?
For example, in this demo: 3.1 Parabolic model problem — NGS-Py 6.2.2302 documentation,
the authors define a so-called m matrix, from which they define an mstar matrix of same size and sparsity, whose inverse they use in the time-stepping loop. Do I have to define two separate m matrices?
However, it is not clear to me how I would go about working with two trial functions and two test functions.
My weak form is:
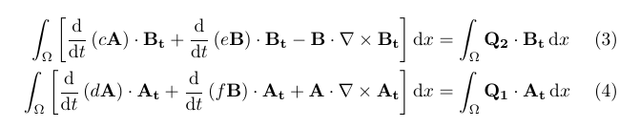
and I am hoping to solve for A and B simultaneously using H-curl elements in a 3D cube.
I apologize if the solution to my confusion is trivial, I am still trying to figure NGSolve out. I attempted this using FEniCS by following their tutorial here: Solving PDEs in Python - <br> The FEniCS Tutorial Volume I (and I made a functional program).
I would appreciate any advice. I understand that my equations might be cryptic and not even be well-posed, but this is mainly an exercise of understanding NGSolve functionality, to me. This is in preparation for research on more-realistic problems.